![[데이터 분석] 선형회귀 / 다항회귀](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbwCsB2%2FbtrPB1JZvPL%2FY3kZ2Qt1VAfgwGyqYOL330%2Fimg.png)

[데이터 분석] 선형회귀 / 다항회귀Data Analysis2022. 10. 26. 23:00
Table of Contents
반응형
요번 포스팅에서는 BOSTON Dataset으로 선형회귀와 다항회귀 분석을 해보겠습니당! ☺️
1. 선형회귀
선형회귀 부터 해볼껀데 우선 쉽게 pandas 에 기본으로 내장되어 있는 boston dataset 을 불러옵니다.
0. Library
#preprocess
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
#visualization
import seaborn as sns
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score1. Load data / EDA
boston = load_boston()
bostonDF = pd.DataFrame(boston.data, columns=boston.feature_names)bostonDF['PRICE'] = boston.target
print('Boston 데이터 세트 크기 :', bostonDF.shape)
# Boston 데이터 세트 크기 : (506, 14)# 각 컬럼이 회귀 결과에 미치는 영향이 어느 정도인지 시각화
fig, axs = plt.subplots(figsize=(16,8), ncols=4, nrows=2)
lm_feature = ['ZN', 'INDUS', 'NOX', 'RM', 'AGE', 'RAD','PTRATIO','LSTAT']
for i, feature in enumerate(lm_feature):
row = int(i/4)
col = i%4
sns.regplot(x=feature, y='PRICE', data=bostonDF, ax=axs[row][col])
print('다른 컬럼보다 RM(양의 선형성), LSTAT(음의 선형성)와 PRICE의 영향도가 큼.')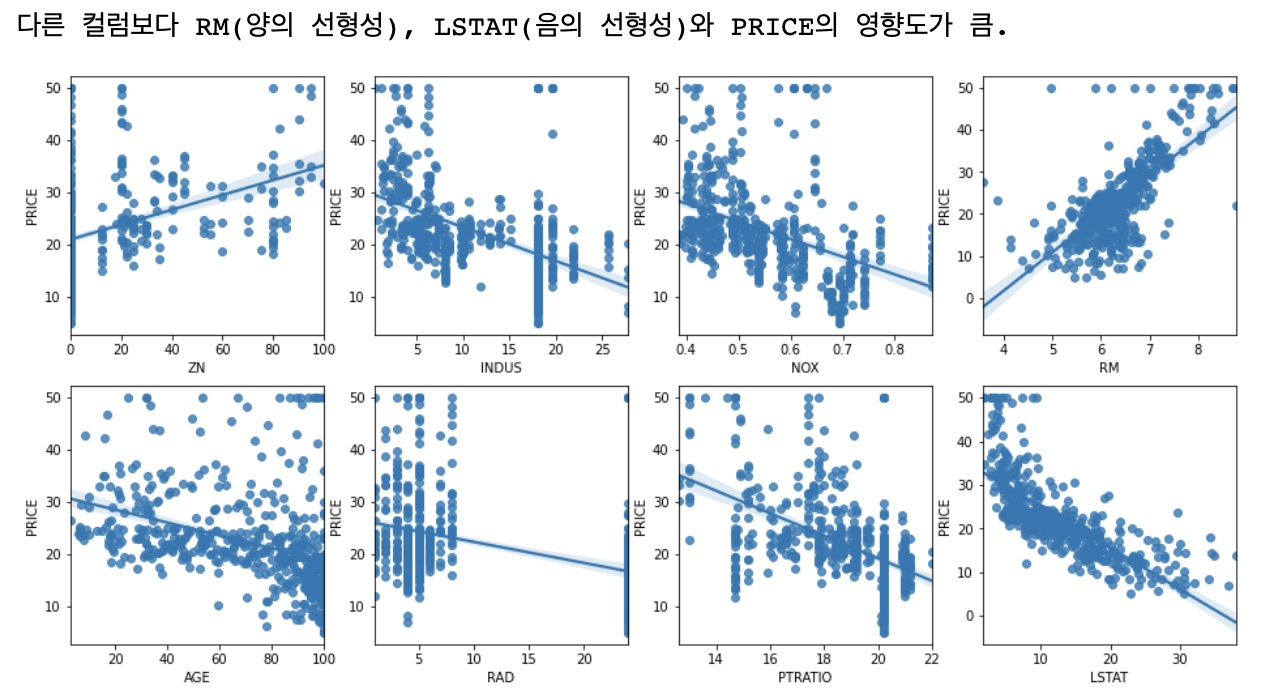
# 주택가격의 회귀모델을 만듬
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
y_target = bostonDF['PRICE']
X_data = bostonDF.drop(['PRICE'], axis=1, inplace=False)
X_train, X_test, y_train, y_test = train_test_split(X_data, y_target, test_size=0.2, random_state=777)
lr = LinearRegression()
lr.fit(X_train, y_train)
pred = lr.predict(X_test)
# metric : mse, rmse
mse = mean_squared_error(y_test, pred)
rmse = np.sqrt(mse)
print('MSE : {0:.3f}, RMSE : {1: .3f}'.format(mse, rmse))
print('Variance score : {0:.3f}'.format(r2_score(y_test, pred)))
# MSE : 24.368, RMSE : 4.936
# Variance score : 0.682r2값이 0.682이므로 약 68.2%의 설명력을 가진다고 말할 수 있다.
Regression metric 설명
- MSE (Mean square error): ( 실제값 - 예측값 ) ^2 의 평균
- RMSE (Root Mean square error): MSE 값이 차이의 제곱을 구하므로 실제 오류 평균보다 더 커지는 특성이 있기 때문에 MSE에 루트를 씌운것이 RMSE이다.
- R2 score : 분산 기반으로 예측 성능을 평가. 실제 값의 분산 대비 예측값의 분산 비율을 지표로 하며, 1에 가까울수록 예측 정확도가 높다. 예측값 variance / 실제 값 variance
log를 취한 값의 metric - MSLE (Mean Squared Log Error) : log를 취한 값에 MSE를 해준 것.
- RMSLE (Root Mean Square Logarithmic Error) : log를 취한 값에 RSME를 해준 것.
결정계수 (Coefficient) 란?
회귀 모델이 주어진 자료에 얼마나 적합한지를 평가하는 지표.
y의 변동량 대비 모델 예측값의 변동량을 의미. 0~1사이의 값을 가지며, 상관관계가 높을 수록 1에 가까운 값을 가짐.
r2 = 0.3이면 30%의 설명력을 가진다고 할 수 있다.
# Linear Regression으로 생성한 주택가격 모델의 intercept(절편), coefficient(회귀계수) 값을 보기.
# PCA할때 coef를 확인하여 주성분만 모델링 하기도 함.
# 절편 값: 40.70998004268002
# 회귀 계수값 : [ -0.1 0. -0. 3. -19.4 3.5 -0. -1.6 0.3 -0. -0.9 0.
-0.6]
print('절편 값:', lr.intercept_)
print('회귀 계수값 :', np.round(lr.coef_,1))회귀 계수를 확인해보자.
coeff = pd.Series(data=np.round(lr.coef_, 1), index=X_data.columns)
coeff.sort_values(ascending=False) #오름차순 정렬
#RM 피처의 회귀 계수가 가장 큼.
RM 3.5
CHAS 3.0
RAD 0.3
B 0.0
TAX -0.0
AGE -0.0
INDUS -0.0
ZN 0.0
CRIM -0.1
LSTAT -0.6
PTRATIO -0.9
DIS -1.6
NOX -19.4
dtype: float642. 다항회귀
독립변수와 종속변수의 관계가 일차 방정식 형태로 표현된 회귀이다. 2차 3차 방정식과 같은 다항식으로 표현되는 것을 다항 회귀라고 함. (다항 회귀도 선형회귀임.)
선형 회귀(직선)보다 다항 회귀(2차 3차 방정식)으로 표현하는 것이 예측 성능이 더 좋음.
하지만, 다항식의 차수가 높아질 수록 학습 데이터에만 너무 맞춘 학습이 이뤄져서 정작 테스트 데이터 환경에서는 오히려 예측 성능이 떨어짐. → Overfitting 문제 발생할 수 있음.
# X = 학습 데이터 30개 , y = noise가 포함된 다항식의 코사인의 그래프 관계를 가지도록 만들어줌.
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import Pipeline
def true_fn(X):
return np.cos(1.5 * np.pi * X)
np.random.seed(0)
n_samples = 30
X = np.sort(np.random.rand(n_samples))# np.random.rand : 0~1 사이의 균일 분포에서 난수 생성. randn : 가우시안 정규 분포에서 난수 생성
# y값은 노이즈 섞어줌
y = true_fn(X) + np.random.randn(n_samples) * 0.1
plt.figure(figsize = (14,5))
# 차수 3가지
degree = [1, 4, 15]
for i in range(len(degree)):
ax = plt.subplot(1, len(degree), i+1)
plt.setp(ax, xticks=(), yticks=())
# 개별 degree를 polymonial로 변환
polynominal_degree = PolynomialFeatures(degree=degree[i], include_bias=True)
lr = LinearRegression()
pipline = Pipeline([("polynomial_feature", polynominal_degree),
("linear_regression", lr)])
pipline.fit(X.reshape(-1,1), y)
# 교차검증
score = cross_val_score(pipline, X.reshape(-1,1), y, scoring='neg_mean_squared_error', cv=10)
coeff = pipline.named_steps['linear_regression'].coef_
print('\nDegree {0} 회귀 계수는 {1} 입니다.'.format(degree[i], np.round(coeff,2)))
print('Degree {0} MSE는 {1} 입니다.'.format(degree[i], -1*np.mean(score)))
#테스트 데이터 세트에 회귀 예측을 수행하고, 예측 곡선과 실제 곡선을 비교.
X_test = np.linspace(0,1,100)
#예측값 곡선
plt.plot(X_test, pipline.predict(X_test[:, np.newaxis]), label="Model")
#실제값 곡선
plt.plot(X_test, true_fn(X_test), "--", label="True Prediction")
plt.scatter(X, y, edgecolor='b', s=20, label='samples')
plt.xlabel("x")
plt.ylabel("y")
plt.xlim(0,1)
plt.ylim(-2,2)
plt.legend(loc='best')
plt.show()
이렇게 정당한 degree가 decision boundary를 잘 나눠주는 것을 볼 수 있다. degree가 너무 높으면 trainset 데이터 각각에 대한 오버피팅을 일으킨다.
728x90
반응형
'Data Analysis' 카테고리의 다른 글
| [데이터 분석] 라벨 불균형 처리 (0) | 2022.10.28 |
|---|---|
| [데이터 분석] 이상치 처리 (0) | 2022.10.28 |
| [데이터 분석] 모델 성능 향상 (0) | 2022.10.28 |

@부지런깨꾹이 :: Gaegul's devlog
Action speaks louder than words. 하루 하루의 기록을 습관화 합니다 📖
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!
![[데이터 분석] 이상치 처리](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FHtw3z%2FbtrPJ4ZA2jh%2Ff481ElVW9SzJXujDVjJ5a0%2Fimg.png)
![[데이터 분석] 모델 성능 향상](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fc3tNFV%2FbtrPK1aaVRU%2FiBZ0gyauWRArv9jHD4JVZ0%2Fimg.png)