![[Algorithom 개념] Binary Tree(트리)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbuEKQA%2FbtrO9z05F1a%2Fw26KPZgtIm9ywSXdOHbmLk%2Fimg.png)

[Algorithom 개념] Binary Tree(트리)Algorithm/Algorithm 개념2022. 10. 21. 01:03
Table of Contents
반응형
1) 트리 (Tree) 란?
트리는 가계도와 같은 계층적인 구조를 표현할 때 사용할 수 있는 자료구조
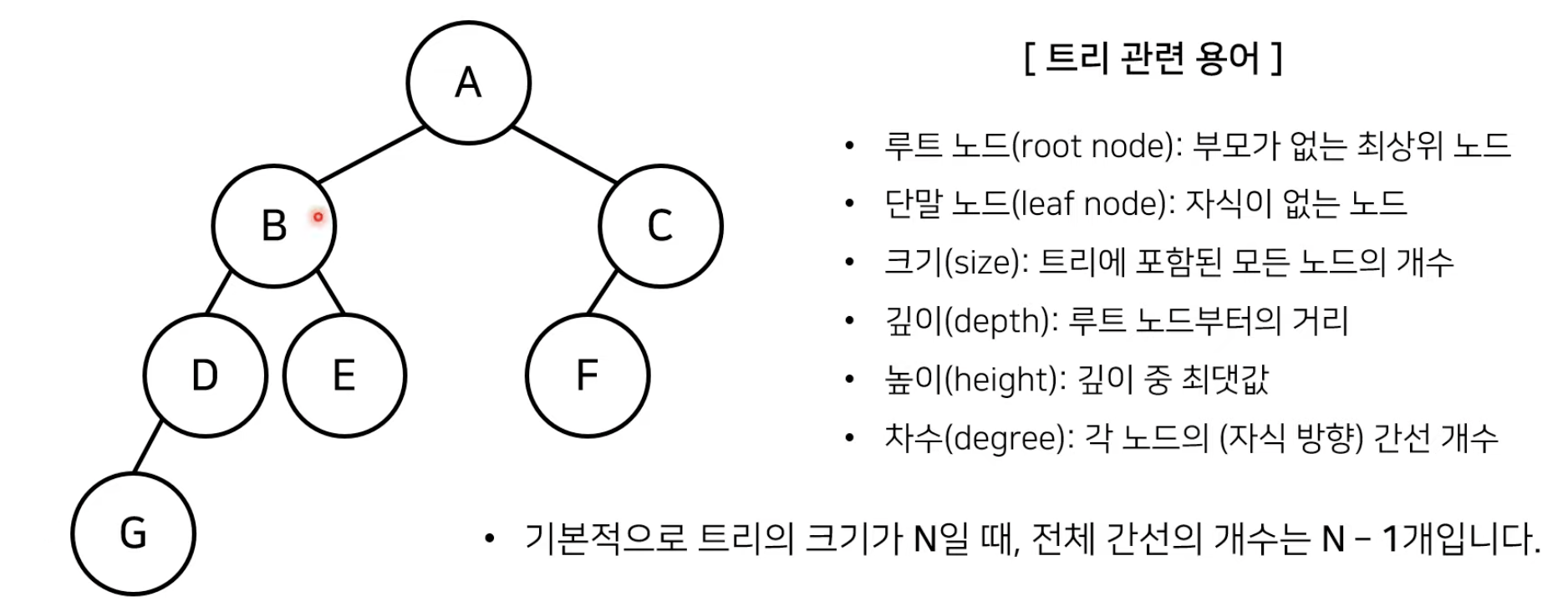
2) 이진 탐색 트리 (Binary Search Tree) 란?
이진 탐색이 동작할 수 있도록 고안된 효율적인 탐색이 가능한 자료구조의 일종.
이진 탐색 트리의 특징 : 왼쪽 < 부모 < 오른쪽
- 부모 노드보다 왼쪽 자식 노드가 작습니다.
- 부모 노드보다 오른쪽 자식 노드가 큽니다.
3) 트리의 순회 (Tree Traversal)
트리 자료구조에 포함된 노드를 특정한 방법으로 한 번씩 방문하는 방법.
트리 순회 방법 종류
- 전위 순회 (pre-order traverse) : root - left -right
- 중위 순회 (in-order traverse) : left - root - right
- 후위 순회 (post-order traverse) : right - root - left
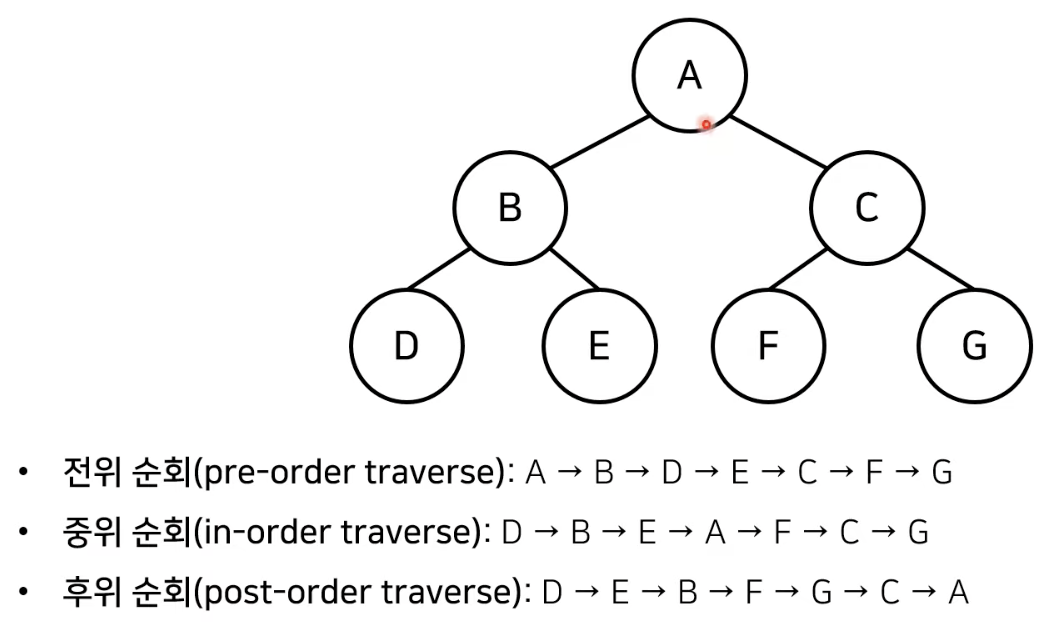
대표 문제 1. 트리 순회 출력하기
문제
루트가 0인 이진트리가 주어질 때, 이를 전위순회, 중위순회, 후위순회한 결과를 각각 출력하는 프로그램을 작성하시오.
입력
첫 번째 줄에 트리의 노드 개수 n이 주어진다. ( 1 ≤ n ≤ 100 ) 두 번째 줄부터 트리의 정보가 주어진다. 각 줄은 3개의 숫자 a, b, c로 이루어지며, 그 의미는 노드 a의 왼쪽 자식노드가 b, 오른쪽 자식노드가 c라는 뜻이다. 자식노드가 존재하지 않을 경우에는 -1이 주어진다.
예제 입력
6
0 1 2
1 3 4
2 -1 5
3 -1 -1
4 -1 -1
5 -1 -1
예제 출력
0 1 3 4 2 5
3 1 4 0 2 5
3 4 1 5 2 0
CODE
딕셔너리로 쉽게 구현함.
#전위 #root-left-right
def pre_order(N):
global graph
if N in graph:
print(N, end=" ")
pre_order(graph[N][0])
pre_order(graph[N][1])
#중위 #left-root-right
def in_order(N):
global graph
if N in graph:
in_order(graph[N][0])
print(N, end=" ")
in_order(graph[N][1])
#후위 #left-right-root
def post_order(N):
global graph
if N in graph:
post_order(graph[N][0])
post_order(graph[N][1])
print(N, end=" ")
N = int(input())
graph = {}
for i in range(N):
root, left, right = map(int, input().split())
graph[root] = [left, right]
#출력
pre_order(0)
print()
in_order(0)
print()
post_order(0)
728x90
반응형
'Algorithm > Algorithm 개념' 카테고리의 다른 글
| [Algorithm 개념] 다익스트라 알고리즘 (최단거리) (0) | 2022.10.12 |
|---|---|
| [Algorithm 개념] binary search (이진 탐색) (0) | 2022.08.26 |
| [Algorithm 개념] DFS / BFS (0) | 2022.08.24 |
| [Algorithm 개념] Greedy Algorithm (0) | 2022.05.17 |
| [Algorithm 개념] Dynamic Programming (0) | 2022.05.10 |

@부지런깨꾹이 :: Gaegul's devlog
Action speaks louder than words. 하루 하루의 기록을 습관화 합니다 📖
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!
![[Algorithm 개념] Greedy Algorithm](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FeaWwCM%2FbtrCLleL0wi%2FWSKAQlhmQl0fvdosIkBve1%2Fimg.png)