[시계열 분석] ARIMA 예측 모델 , 정상성과 자기상관

1. 정상성 (Stationary) 

시계열 데이터의 특성이 시간의 흐름에 따라 변하지 않는다는 것을 의미. 정상 시계열은 장기적으로 예측 가능한 패턴을 갖지 않으며, 시계열 그래프는 일정한 변동폭(일정한 분산)을 가지며, 대체로 수평에 가까운 패턴(일정한 평균)을 보인다.

즉, 데이터가 정상성을 보인다는 것은 평균과 분산이 안정화 되어 있어 분석하기 쉽다는 것을 의미. 

1) 비정상성(non-stationary) : 추세나 계절요인은 시간이 경과하면서 관측값에 영향을 미치기 때문에 추세 성분이나 계절 성분을 갖는 시계열

(a), (b), (c) 비정상 시계열 (d) 정상 시계열

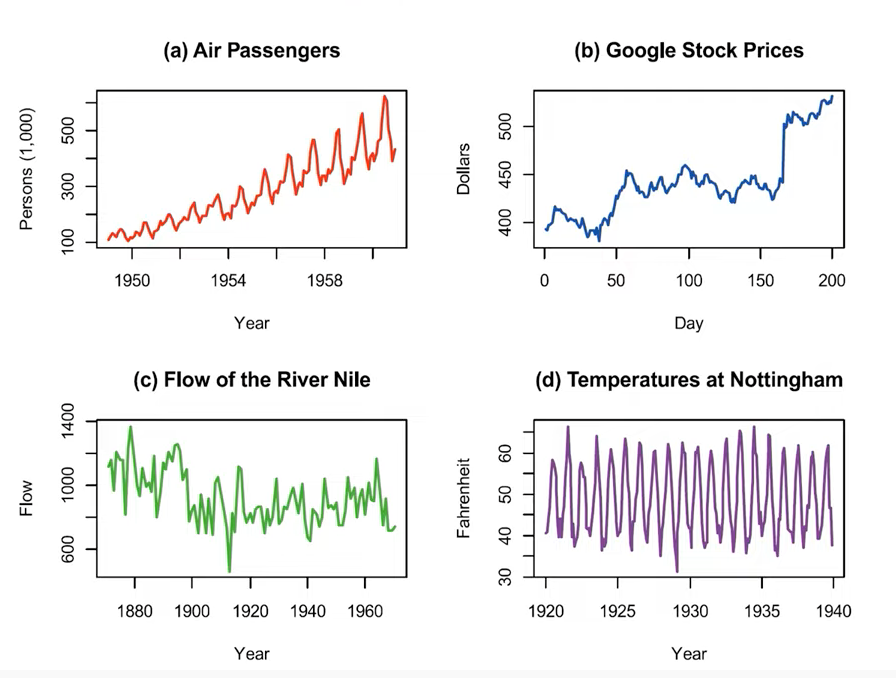
2) 정상성(stationary) : 불규칙 성분만으로 구성된 시계열은 정상적. 어느 시점에서 관찰하든 관측값은 불규칙한 변동을 제외하면 동일한 모습을 가짐.

추세나 계절 요인이 포함되어 있어서 데이터가 정상성을 갖지 않으면, 그러한 복잡한 패턴을 모델링하여 분석하는 것이 어렵기 때문에 일반적으로 정상성을 갖도록 전처리를 수행해야 한다.

2. 자기상관

정상 시계열은 어느 시게열 구간에서 관찰하든 평균과 분산이 일정하며, 또한 관측값 간의 공분산도 일정 => 자기 상관(autocorrelation) 이 시간에 따라 변화하지 않는다는 것을 의미. 자기 상관은 동일한 변수를 시점을 달리하여 관찰하였을 때 이 관측값들 사이의 상호 관련된 정도를 나타내는 척도.

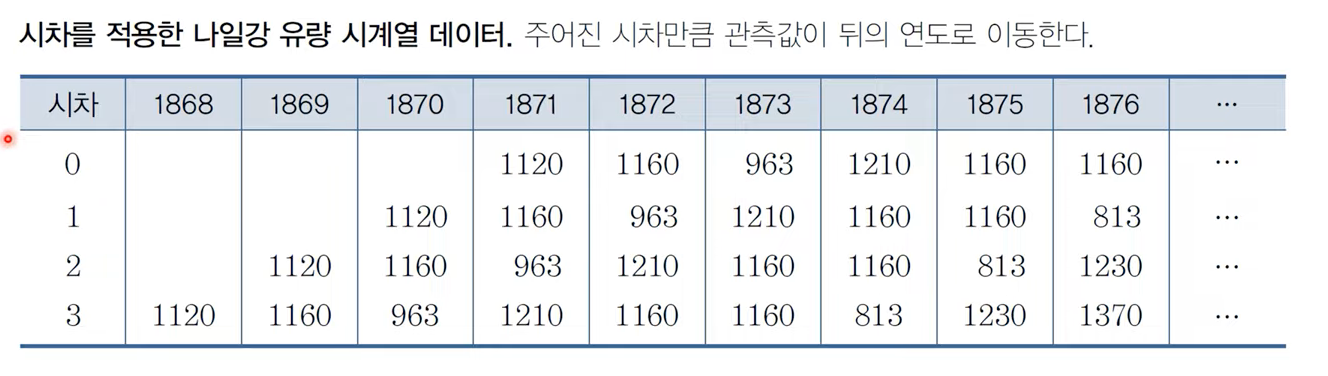
• 자기 상관은 시차(lag)를 적용한 시계열 데이터를 이용하여 계산.
• 시차를 적용한다는 것은 특정 시차만큼 관측값을 뒤로(즉, 과거의 시점으로) 이동시키는 것을 의미.

자기 상관은 다른 시점의 관측값 간의 상호 연관성을 나타내므로, 이는 시차를 적용한 시계열 데이터간의 상관관계를 의미.

자기 상관 ACk는 원래의 시계열 데이터(yt)와 k시차가 고려된, 즉 k 기간 뒤로 이동한 시계열 데이터(yt-k) 간의 상관관계로 정의할 수 있음. e.g. AC1는 시차 0 시계열 데이터와 시차 1 데이터간의 상관관계.

 

3. 자기상관함수 (ACF)

1. 시차에 따른 일련의 자기상관 {AC1, AC2, ... ACk}를 자기상관함수라고 한다. 

2. ACF는 시차에 따른 관측값 간의 연관 정도를 보여주며, 시차가 커질수록 ACF는 점차 0에 가까워지게 됨. 

3. ACF 는 시계열의 정상성을 평가할 때 유용.

• 정상 시계열의 ACF는 상대적으로 빨리 0으로 감소
• 비정상 시계열의 ACF는 천천히 감소하며, 종종 큰 양의 값을 가짐.

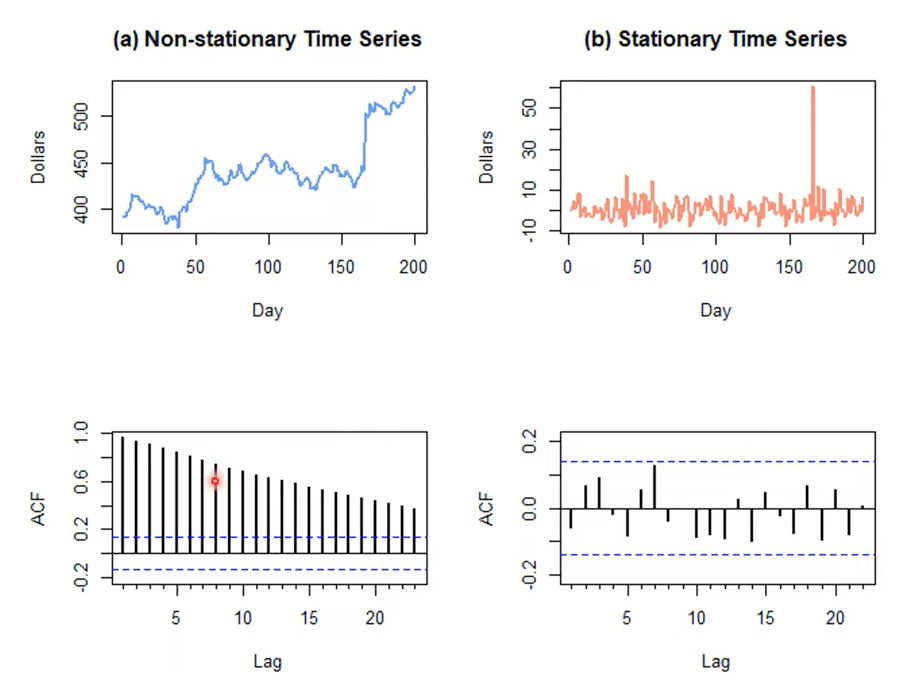
(a) Non-stationary : 비정상 시계열에 대응되는 ACF 도표는 자기상관이 크고 양수이며, 천천히 감소하는 패턴

(b) Stationary: 정상 시계열에 대응되는 ACF 도표는 모든 시차에서 0에 근첩한 자기 상관을 보여줌

 

4. 편자기상관함수 (PACF)

1. 편자기상관(partial autocorrelation)은 시차가 다른 두 시계열 데이터 간의 순수한 상호 연관성을 나타냄.

2. 편자기상관 PACk는 원래의 시계열 데이터 (yt)와 시차 k 시계열 데이터(yt-k) 간의 순수한 상관관계로서 두 시점 사이에 포함된 모든 시계열 데이터의 영향은 제거됨.

3. 시차에 따른 일련의 편자기상관 {AC1, AC2, ... ACk}를 편자기상관함수라고 한다. 

 

5. 정상 시계열로의 변환

1. 변동폭이 일정하지 않으면 로그변환을 통해 시간의 흐름에 따라 분산이 일정하게 유지되는 정상 시계열로 변환.

2. 추세나 계절적 요인이 관찰되면 차분 (시계열 yt의 관측값 : yt - yt-1로 대체)과정을 통해 전 기간에 걸쳐 평균이 일정한 정상 시계열로 변환

3. 변동폭이 일정하지 않고 추세와 계절적 요인 또한 존재하면 로그 변환과 차분 과정을 모두 적용하여 정상 시계열로 변환.

(a) : 변동폭이 일정하지 않고 추세와 계절적 영향이 존재하는 비정상 시계열

(b) : 로그 변환을 통해 좀 더 단순화된 일정한 분산을 갖는 시계열로 변환

(c) : 차분을 통해 0을 중심으로 평균이 일정하게 유지되는 패턴으로 변환

(d) : 로그 변환과 차분을 통해 평균과 분산이 일정하게 유지 되는 정상 시계열로 변환

 

6. ARIMA 예측 모델

ARIMA 예측 모델은 기본적으로 AR와 MA모델을 바탕으로 함. 또한, ARIMA 예측 모델은 시계열 데이터의 정상성을 가진다고 가정.

1) AR 모델

: 시계열상의 과거 관측값을 이용하여 예측 모델 생성

• 예측하고자 하는 특정 변수의 과거 관측값의 선형 결합으로 해당 변수의 미래값 예측
• 과거 p개 관측값의 선형결합으로 예측하는 모델을 p차 AR 모델이라고 하며 AR(p)로 표현

2) MA 모델

: 과거 예측 오차를 기반으로 예측 모델 구축

• 예측 오차를 이용하여 미래의 값 예측
• 과거 q개 예측오차의 선형결합으로 예측하는 모델을 q차 MA 모델이라고 하며 MA(q)로 표현

3) ARMA 모델

• AR(p) 모델과 MA(q)모델을 결합하여 ARMA(p,q) 모델 도출.
• 시계열의 각 값을 과거 p개 관측값과 q개 오차를 이용하여 예측.

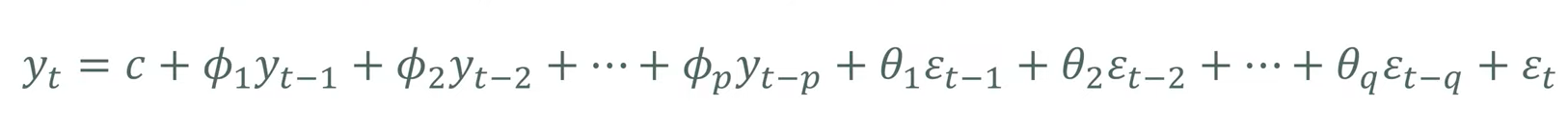
4) ARIMA 모델

: ARMA 모델에 차분과정 추가

• 시계열 데이터를 d회 차분하고 결과값은 과거 p개 관측값과 q개 오차에 의해 예측되는 모델.
• 결과값은 비차분화 과정을 거쳐 최종 예측값으로 결정.

5) ARIMA 모델 선택 예시

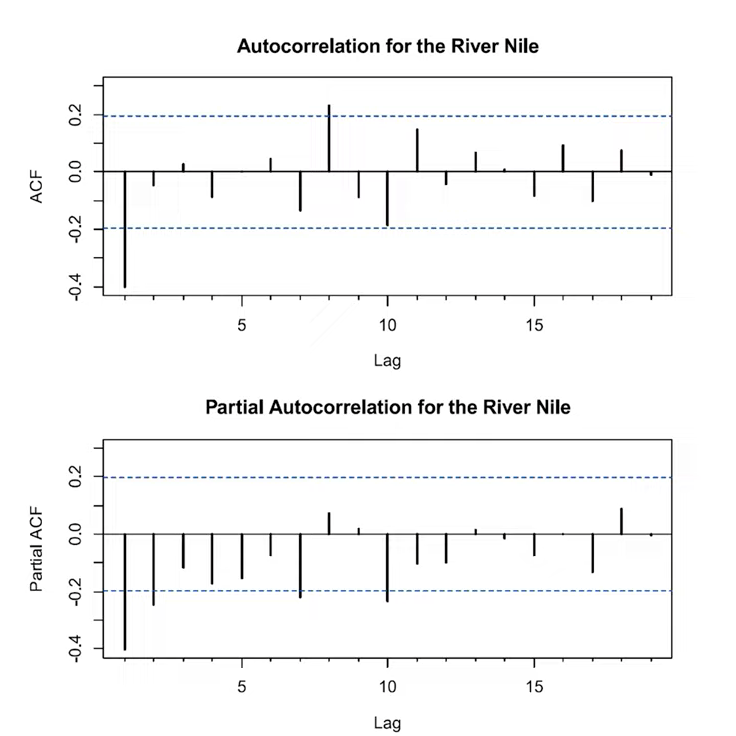
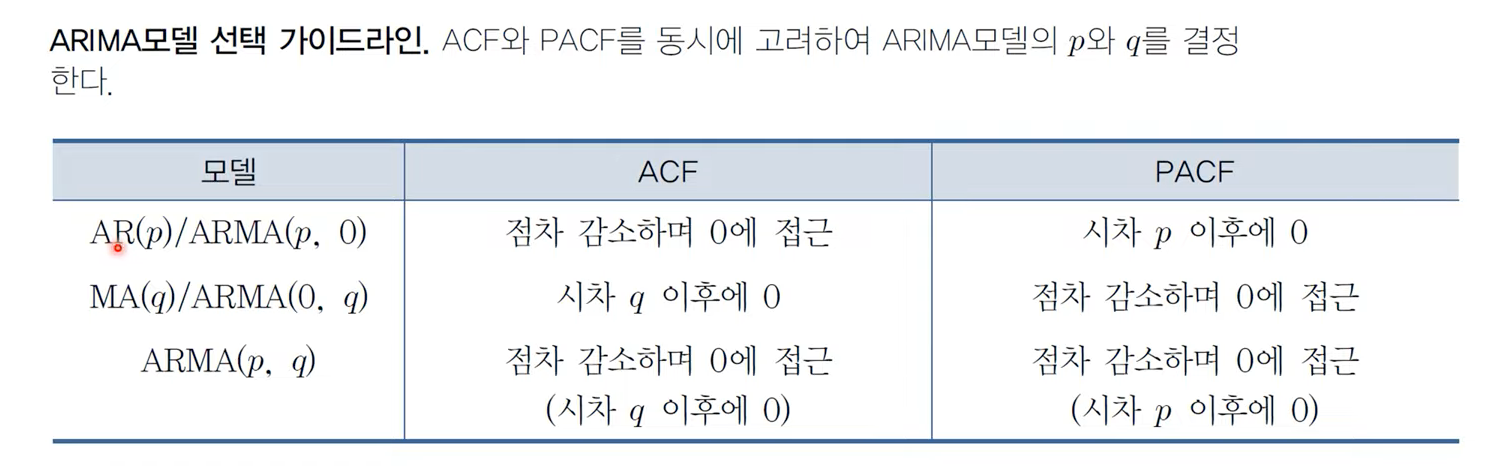
• 자기상관은 시차 1 이후에 0이 되고, 편자기상관은 시차 2 이후에 0이 됨.
• 자기상관과 편자기상관은 모두 점진적으로 0에 이르고 있음.
• 모델 선택 가이드에 따르면, AR(2) / ARMA(2,0), MA(1) / ARMA(0,1), ARMA(2,1) 등의 모델이 가능